오늘은 합성곱 오토 인코더를 구현하는 수업을 들었습니다.
저번 글에서 오토 인코더에 대한 이야기를 하며 잠깐 언급했는데
저번에 이야기했던 오토 인코더에 CNN 아이디어를 도입한 신경망입니다.
CNN은 미국의 뉴스 채널이 아니라 Convolutional Neural Network입니다.
CNN은 ResNet이나 SENet을 예로 보면 이미지 학습에 탁월해서
사람보다 이미지 분류 능력이 뛰어나게 학습도 가능합니다.
이런 이유로 CNN은 이미지 학습에 좋은 성능을 내지 못하는 오토 인코더와 같이 쓰면
오토 인코더의 이미지 학습 성능이 좋아집니다.
오토 인코더의 구조는 인코더와 디코더로 이루어져 있다고 저번에 이야기했었는데요.
적층으로 구성될 때는 이 구조가 대칭이어서 인코더에서 뉴런이 줄었다면
디코더에서는 뉴런이 줄은 만큼 늘어야 입력층과 같은 사이즈의 출력층을 갖게 됩니다.
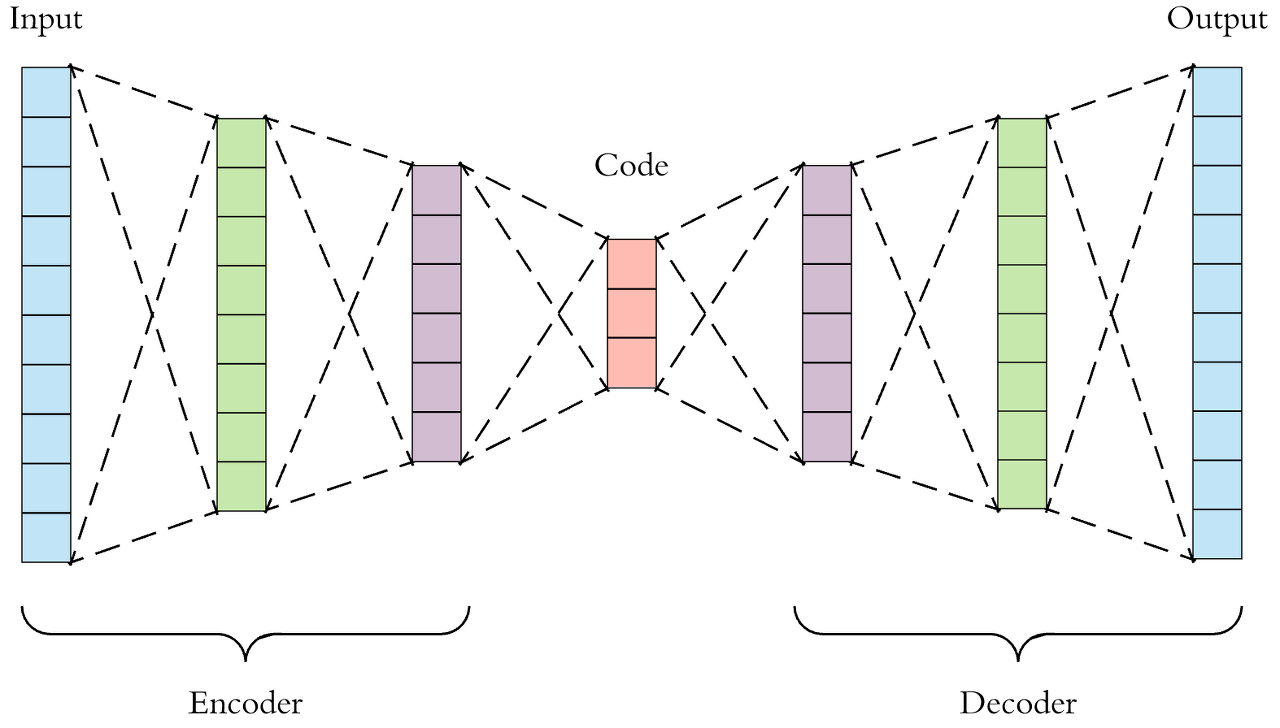
이와 같은 논리로 Convolutional Autoencoder(합성곱 오토 인코더)도 인코더와 디코더의 구조가 대칭입니다.
CNN은 일반적으로 합성곱층과 풀링층을 거치면서 높이와 너비가 줄어들고 깊이가 늘어납니다.
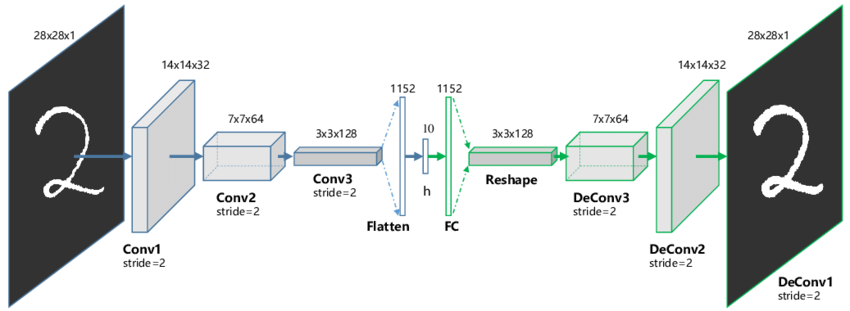
아래의 그림처럼 Convolution, RELU, Pooling을 지나며 가로 세로는 작아지고 깊이는 깊어지는 게 특징입니다.

오토 인코더 구조의 인코더 부분은 이러한 CNN구조가 그대로 대입됩니다.
그래서 입력 데이터는 인코더가 끝나는 부분에서 가로, 세로는 작고 두꺼운 데이터가 됩니다.
오토 인코더의 인코더와 디코더는 대칭 구조로 되어있기 때문에
디코더 부분에서는 다시 가로와 세로를 키워주고 얇게 펴주는 작업이 필요합니다.
이러한 합성곱을 Transposed Convolution이라 부릅니다.
Transposed Convolution은 Convolution(합성곱)을 역연산하는 것이 아니라 "Upsampling" 하는 게 주목표입니다.
단순히 역연산을 한다면 input과 완전히 같은 데이터가 생성되기 때문에 학습의 의미가 없어집니다.
Deconvolution과 Transposed Convolution의 차이가 헷갈릴 수도 있습니다.
Deconvolution은 역순으로 연산해 연산 전의 인풋 데이터로 되돌아가는 것으로 볼 수 있고
Transposed Convolution은 학습으로 생성된 파라미터로 공간 차원을 늘린다고 볼 수 있습니다.
아래의 움짤을 보면 그 원리를 이해하기 더 쉬운데요.
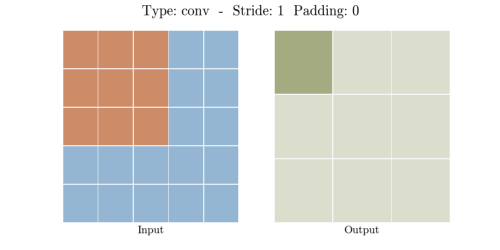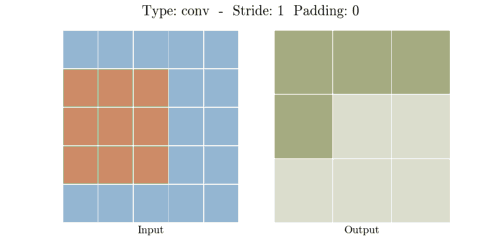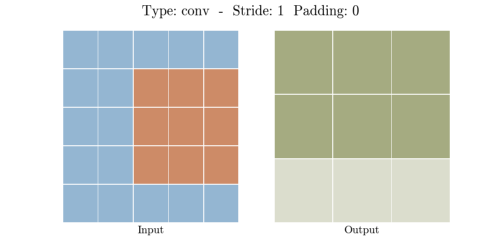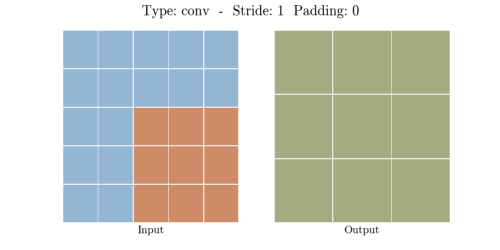
Convolution layer에서 3*3 커널이 인풋 데이터를 내적 계산을 통해 공간 차원을 줄입니다.
5*5 픽셀이 Convolution Layer를 지나 3*3픽셀이 된 것을 알 수 있습니다.
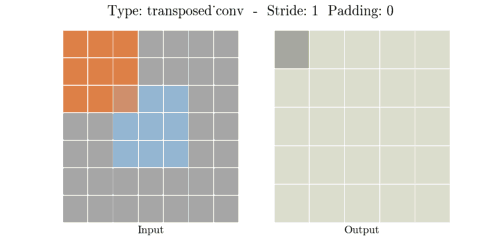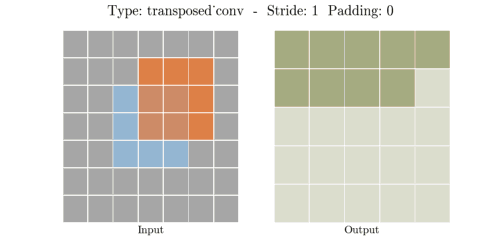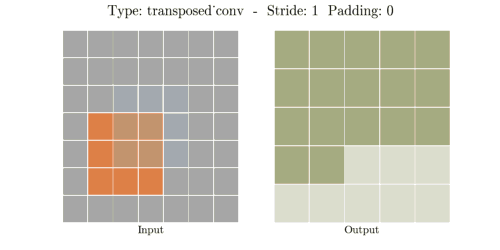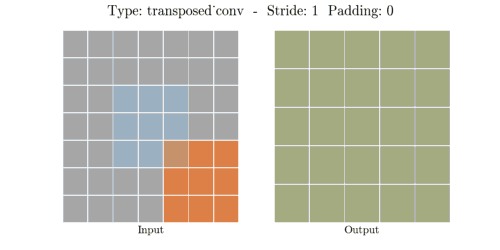
Transposed Convolution은 역연산이 아니라 위와 같은 방법으로 공간 차원을 늘립니다.
(stride - 1) 만큼 input 사이의 열과 행에 0을 채워 넣어 인풋 공간 차원을 증가시키고 --> 0
(kernel - padding - 1)만큼 0으로 패딩(테두리 늘림) 하여 인풋 공간 차원을 증가시킵니다. --> 2
공간 차원을 증가시킨 input data에 convolution 연산을 하여 output을 출력합니다.
위에서 설명한 Convolution Layer와 Transposed Convolution Layer를 Encoder, Decoder에 넣어서
오토 인코더에게 꽤 높은 퀄리티의 이미지 학습을 시킬 수 있습니다.
Pytorch에서 이를 구현한 코드입니다.
아래서 구현된 코드의 이미지 차원은
input(3*32*32) --> ecoder [conv1(16*32*32) --> pool(16*16*16) --> conv2(32*16*16) --> pool(32*8*8)]
--> decoder [transconv1(16*16*16) --> transconv2(3*32*32)] --> output(3*32*32)
이렇게 차원의 변화가 대칭으로 일어납니다.
class ConvAutoEncoder(nn.Module):
def __init__(self):
super(ConvAutoEncoder, self).__init__()
# Encoder
self.conv1 = nn.Sequential(
nn.Conv2d(in_channels=3, out_channels=16, kernel_size=3, stride=1, padding=1),
nn.SELU(),
nn.MaxPool2d(kernel_size=2, stride=2)
)
self.conv2 = nn.Sequential(
nn.Conv2d(16, 32, 3, 1, 1),
nn.SELU(),
nn.MaxPool2d(2,2)
)
# Decoder
self.transconv1 = nn.Sequential(
nn.ConvTranspose2d(in_channels=32, out_channels=16, kernel_size=2, stride=2),
nn.ReLU(),
)
self.transconv2 = nn.Sequential(
nn.ConvTranspose2d(16, 3, 2, 2),
nn.Sigmoid(),
)
def forward(self, x):
x = self.conv1(x)
encoded = self.conv2(x)
decoded = self.transconv1(encoded)
out = self.transconv2(decoded)
return out
conv_model = ConvAutoEncoder()

Convolution Autoencoder로 생성한 이미지와 원본 이미지가 꽤 비슷한 것을 확인할 수 있습니다.
추가로 input data의 수치 범위와 output data의 수치 범위를 갖게 해 줘야 적절한 학습이 가능합니다.
예를 들면 제가 위에서 구현한 코드는 마지막에 Simoid 활성 함수를 거치기 때문에
output data의 수치 범위는 -1과 1 사이의 값을 가집니다.
그러므로 input data의 수치 범위도 -1과 1 사이로 Normalize 시켜야 합니다.
이것이 지켜지지 않는다면 학습이 잘 안 되는 것은 물론이고 이미지의 품질도 굉장히 떨어집니다.
이걸 또 심화시키면 GAN이 되겠지요..?
오늘 수업에서 짧게 다뤘는데 다음 글에서 저도 짧게 한번 다뤄보겠습니다..
'AI > K-Digital Training' 카테고리의 다른 글
| 027. 딥러닝과 주식투자의 연계성에 대한 인문학적 고찰 (0) | 2021.10.04 |
|---|---|
| 026. GAN(Generative Adversarial Network) 으로 간다 (0) | 2021.10.04 |
| 024. Autoencoder라는 높은 벽 (0) | 2021.10.01 |
| 023. 오마이갓.. 오토인코더 (1) | 2021.09.30 |
| 022. 지도 학습에서 회귀 문제와 분류 문제에 대한 이야기 (0) | 2021.09.30 |