[Coursera: Machine Learning] 3주차 리뷰 - 분류 문제, 과적합 문제

이번 주차에 배운 내용의 분량이 지금까지 강의 중에 가장 많은 것 같습니다. 앤드루 응 교수님께서 괜히 이렇게 갑자기 분량을 늘릴 일은 없습니다. 아마 배우는 패턴이 비슷해지기 때문인 것 같습니다. 머신러닝에서 학습 과정의 전체적인 구조는 변화하지 않기 때문에 이런 패턴으로 배우는 것 같습니다. 같은 패턴에서 수학 공식이 달라지는 식으로 변주되기 때문에 배움에 편의성이 생겨 강의 분량이 많아지는 것 같습니다. 학습의 패턴은 다음과 같습니다. 

 

Hypothesis -> Cost Function -> Descent Gradient

 

이번 주차에 배운 내용들

• Classification
• Hypothesis Representation
• Decision Boundary
• Cost Function(logistic regression)
• Simplified Cost Function and Gradient Descent
• Advanced Optimization
• Multiclass Classification: One-vs-all
• The Problem of Overfitting
• Cost Function(Regularization)
• Regularized Linear Regression
• Normal Equation
• Regularized Logistic Regression

사이킷런을 사용하면 코드 몇 줄로 해결되는 문제라서 어떤 논리로 분류 문제와 과적합(overfitting) 문제가 해결되는지 깊게 고민하지 않았는데 이번에 제대로 한 번 짚고 넘어가게 되었습니다. 사실 패스트캠퍼스에서는 직관적으로 이해하기 어렵게 강의하는 경우가 많다 보니 제가 이런 지경에 이른 게 아닌가 싶기도 합니다. 기계 학습에 사용되는 다양한 수학적인 이론들을 직관적인 이해부터 논리적인 이해(코드)까지 하다 보니 흐름을 제대로 알게 되는 것 같습니다. 아직 이것밖에 안 배웠지만 교수님께서 이제 수업에서 배운 내용으로 실리콘 밸리로 가서 돈 벌 수 있다고 하시니까 당황스럽기는 하지만 기본기는 제대로 다졌구나 싶었습니다.

 

분류 문제

0과 1로 분류하는 분류 문제는 선형 회귀에서 값이 0.5보다 큰 것은 1로 작은 것은 0으로 치환해서 해결할 수 있습니다. 하지만 회귀 문제는 연속되는 값을 구하는 것이 목표이기 때문에 분류 문제를 해결하기 위해 쓰는 것이 굉장히 어렵습니다. 그래서 선형 회귀를 분류 문제에 전용하기 위해 잠시 y 값이 이산적인 값인 것을 무시할 필요가 있습니다. 일단 우리가 구하려고 하는 값이 0과 1이기 때문에 y 값이 0보다 작거나 1보다 큰 경우를 방지하기 위해 우리 가설의 형태를 Logistuc Function(Sigmoid Function)으로 바꿔야 합니다.

이 함수에 대입하게 되면 모든 값이 0과 1 사이에 위치하게 되고 분류 문제를 해결하는 데에도 적합하게 됩니다. 이는 이진 분류 문제에서 우리가 원하는 값이 나올 확률을 알려주게 됩니다. 예를 들어 hθ(x)=0.7라면 결과가 1일 확률이 70%라는 뜻이 됩니다. 반대로 0일 확률은 30%라는 뜻이 됩니다.

 

Decision Boundary

우리의 분류 가설 함수는 다음과 같이 해석할 수 있습니다. y의 값이 0.5보다 크면 1이고 0.5보다 작으면 0입니다.

hθ(x)≥0.5→y=1

hθ(x)<0.5→y=0

 

이를 Logistic Function g에 적용하여 우리의 문제를 풀려면 입력값이 0보다 크거나 같을 때 0.5보다 커야 하므로 다음의 식을 얻을 수 있습니다. 

z=0, e0=1 ⇒ g(z)=1/2

z→∞, e^−∞→0 ⇒ g(z)=1

z→−∞, e^∞→∞ ⇒ g(z)=0

 

Decision Boundary는 y 값이 0인 영역과 1인 영역을 나누는 우리가 만든 가설 함수에서 비롯된 선입니다. Decision Boundary 역시 직선일 필요는 없습니다. 값을 잘 분류할 수만 있다면 곡선이거나 원이여도 됩니다. 하지만 너무 학습 데이터에 과적합되면 새로운 데이터를 예측할 때 문제가 되므로 주의해야 합니다.

 

Cost Function

분류 문제에서는 비용 함수를 선형 회귀와는 다르게 써야 합니다. 비용 함수 특성상 그래프 모양이 볼록한 함수가 아니라 local optima가 생겨서 학습 시에 global optima를 못 구하게 될 수도 있기 때문입니다. 대신에 다음과 같은 형태의 비용 함수를 적용합니다.

 

분류문제에서 비용함수

 

만약 y = 1인 함수의 경우 1일 확률이 0에 수렴할수록 비용 함수는 무한에 가까워집니다.

만약 y = 0인 함수의 경우 0일 확률이 0에 수렴할수록 비용함수는 무한에 가까워집니다.

구하는 값에서 멀어질수록 비용 함수가 증가하므로 우리가 학습 시에 원하는 값(Gradient Descent)을 얻을 수 있게 됩니다.

 

이진 분류 문제에서의 비용 함수는 구하려는 y 값이 무엇인지에 따라 두 개로 나눠지는데 편리하게 이를 하나의 식으로 합칠 수 있습니다. 이렇게 식을 바꾸면 y =1일 때 뒤의 함수는 지워지고, y = 0이면 앞의 함수가 지워집니다.

 

경사 하강법 함수는 비용 함수를 편미분 해서 얻을 수 있습니다. 그러므로 다음과 같은 형태를 가집니다. 분류 문제에서도 역시 선형 회귀와 마찬가지로 모든 세타 값을 동시에 업데이트해줘야 합니다. 하지만 이는 세타를 최적화하는 방법 중 하나일 뿐이므로 우리가 쓰는 툴에서 제공하는 다양한 라이브러리를 활용해 'Conjugate Gradient', 'BFGS' 같은 다른 방법을 써도 좋습니다. 솔직히 저는 이것에 대해 처음 들어봤습니다..

 

다종류 분류

지금까지 이진 분류 문제만을 다뤘는데 지금까지 배웠던 방법들을 총동원하여 다종류 분류 문제도 해결할 수 있습니다. 간단하게도 가설 함수의 개수를 분류할 종류의 개수만큼 늘리면 됩니다. 일단 한 종류와 나머지를 구분하는 함수(이진 분류 함수)를 여러 개 만들면 이론적으로 다종류 분류 문제도 해결할 수 있게 됩니다.

 

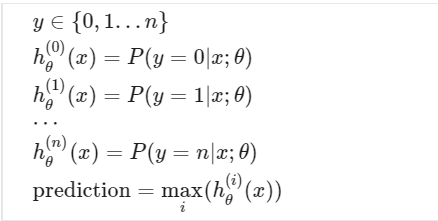
과적합 문제

분류 문제에서 벗어나 회귀 문제를 다시 들여다봅니다. 단순 직선의 경우 데이터에 정확하게 부합하지 않으므로 underfiting 하는 모습을 보여줍니다. 그러나 feature가 많아져서 구불구불한 형태로 모든 데이터에 부합하게 되면 학습 데이터에 overfitting 하게 됩니다. 이는 향후 새로운 데이터의 예측이 부정확하게 할 가능성이 있습니다. 그러므로 우리는 이 사이에서 적절한 값을 구해야 합니다. 물론 이 용어(underfitting, overfitting)는 분류 문제에서도 적용됩니다. 

 

과적합의 문제가 발생했을 경우 두 가지 방법을 사용해 해결할 수 있습니다. 

1. Feature 개수 줄이기(중요한 feature들만 남기기)
2. 정규화(Feature는 유지하고 세타 값을 낮추기)

 

다음과 같은 함수의 과적합 문제를 해결하기 위해 우리가 구한 가설 함수를 변형시키기보다는 비용 함수를 변형해 과적합 문제를 해결합니다. 원래의 비용 함수식 뒤에 두 개의 항을 추가해 θ3과 θ4의 비용을 증가시킵니다. 이를 통해 비용 함수를 최소한으로 줄여도 비용 함수가 0에 수렴하지 않기 때문에 과적합을 방지할 수 있습니다.

θ0+θ1x+θ2x2+θ3x3+θ4x4

 

 

다음과 같은 비용 함수로 모든 세타 파라미터를 정규화시킬 수 있습니다.  람다는 정규화 파라미터인데, 이는 우리의 세타 파라미터가 얼마나 오를지 결정하게 됩니다. 이를 통해 함수를 더 매끄럽게 바꿔 과적합 문제를 해결할 수 있습니다. 만약 람다가 너무 크게 설정되면 너무 함수가 매끄러워져 underfitting 될 수도 있고, 아마 람다가 0에 수렴하면 과적합 문제에 다시 직면할 수도 있습니다.

 

정규화

우리는 선형 회귀, 로지스틱 회귀 모두에 정규화를 적용할 수 있습니다. 이는 다음의 식과 같이 경사 하강 함수에서 θ0을 다른 파라미터들과 분리시킴으로써 가능하게 됩니다. 

 

다음 식에서 앞부분을 통해 정규화를 진행하는데 (1 - a * l/m)의 값은 항상 1보다 작습니다. 이를 통해 경사 하강법을 계속 진행한다면 θj의 값은 매 업데이트마다 작아진다는 것을 알 수 있습니다. 

 

정규 방정식에서 정규화를 적용하려면 원래의 식에서 하나를 추가해야 합니다. 여기서 추가되는 L은 하나는 0인 대각 행렬입니다. 여기서 흥미로운 점은 원래 X^TX의 열이 행보다 더 많다면 비가역성이 있지만 X^TX + λ⋅L은 가역성이 생긴다는 것입니다.

 

로지스틱 회귀의 정규화는 선형 회귀의 정규화와 거의 같은 방법으로 이루어집니다. 아래와 같은 모습으로 과적합된 함수를 정규화시킬 수 있습니다. 이 식에서도 역시 θ0를 제외하고 비용 함수를 변형합니다. 왜냐하면 θ0는 편향이기 때문입니다. 그다음 경사 하강법의 적용 방법은 선형 회귀와 같습니다.